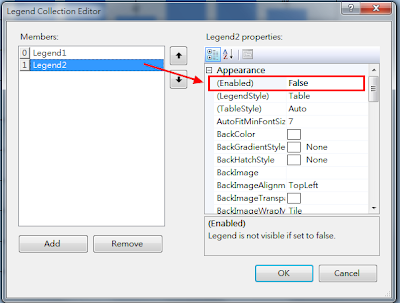
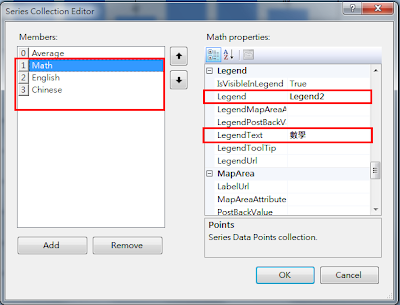
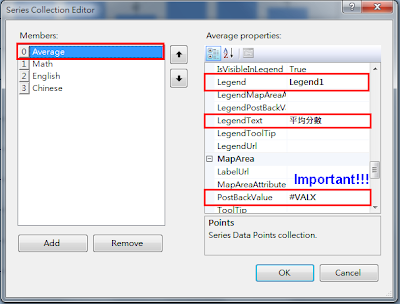
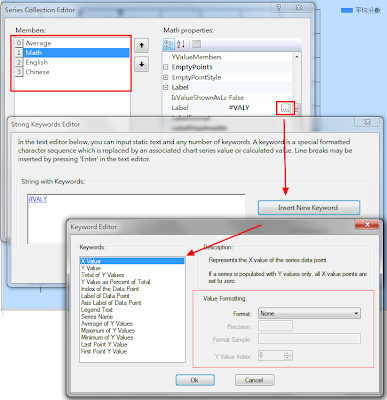
這個證明使用的是反證法(proof by contradiction),以及引理(Lemma)這個以前沒注意過的概念,推導的過程需要相當的邏輯能力,蠻精采的,因此趁機整理一下。
由於數學歸納法適用的問題是自然數命題,因此需要對自然數的基本性質有一定的了解,這部份的補充說明請參考中原大學數學系董世平教授所寫的數學歸納法一文中關於「皮阿諾公設」的說明。
在了解了自然數的基本性質以後,接下來看一下數學歸納法的證明過程(字蠻小的,可能需要另開視窗):

(此證明在研究所考試中曾經考過:91交大資科, 93中原資工)
反證法真的很有趣,比起一般的數學推導(化繁為簡、化簡為繁),欲使用反證法需要有很強的邏輯觀念,最普遍的應用是證明存在性或無限多等無法明確描述的觀念有關的問題,例如:證明正整數中有無限多個質數。因為這個命題是「無限多」,因此無法直接將所有質數表列出來證明(根本表列不完),要驗證此命題是否正確,就必須先假設質數是有限個(故意假設錯誤),再推導出矛盾的結果,進而反證此命題為真。
(存在性問題也是類似的概念,因為沒辦法直接證明「不存在」,因此必須先假設存在,再導出矛盾的結果,進而反證確實不存在)
數學歸納法的應用除了證明一次方連加、二次方連加、三次方連加等公式以外,在 Wikipedia 上面還可以看到應用在 computer science, graph theory 中的變形(稱作 Structural induction (中文)),這部份我還沒學到,所以先略過不談 XD
數學歸納法在使用上要特別小心,若邏輯觀念不夠清楚,使用時可能會產生以下的錯誤,進而推導出奇怪的謬論--利用數學歸納法證明飯永遠吃不飽(原文請參考國立中央大學教學網):

先想想看這個顯然是胡扯的證明到底錯在哪裡?好好思考之後再看一下解答,對於建立邏輯觀念有很大的幫助。(更多的數學歸納法使用錯誤範例請參考:大葉大學通訊與計算機工程學系的許介彥教授的數學歸納法使用上易犯的錯誤一文)
另一個更深入的應用是「如何找出劣幣」(原文請參考台大數學系蔡聰明教授的如何找出劣幣-簡介訊息與熵的概念一文),這跟最近唸資料結構/演算法時碰到的 Decision tree 也有關連,由於我沒辦法解釋的比蔡教授更清楚,所以這邊也略過不談 :p
數學歸納法的部份就先整理到這邊,下一篇預計整理的是「整數和偶數的個數相同」的相關問題。